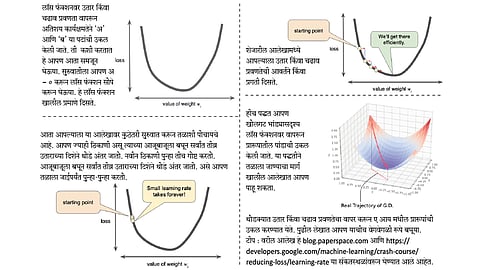

आपण रेषीय प्रतिगमन अर्थात लिनिअर रिग्रेशन या तंत्राविषयी माहिती घेतली. पहिल्या लेखात तोंडओळख आणि मागच्या लेखात त्याविषयीच्या तांत्रिक बाजू! आजच्या लेखात आपण प्रारूपांतील पदांची उकल ऑप्टिमिझेशन या तंत्राने कशी करतात याची माहिती घेऊया.
उजळणीदाखल आपण पुढील रेषीय समीकरणाचा प्रारूप म्हणून उपयोग केला. किंमत = अ + ब * क्षेत्रफळ. ढोबळमानाने य = अ + ब * क्ष. तालीम संचामध्ये आपल्याला ‘क्ष’ आणि ‘य’ यांच्या किमती दिलेल्या असतात आणि आपल्याला भविष्यामध्ये दिलेल्या ‘क्ष’साठी ‘य’ची किंमत शोधून काढायची आहे. मागच्या भागात आपण ‘लॉस फंक्शन’ या संकल्पनेचा वापर करून ‘अ’ आणि ‘ब’ या पदांची कशी उकल करावी याचा उहापोह केला. हे काम कार्यक्षमपणे करण्यासाठी ऑप्टिमिझेशनमधील काही संकल्पनांचा वापर होतो. ऑप्टिमिझेशन ही गणिताची एक उपशाखा आहे. इथे मला एक गोष्ट नमूद करावीशी वाटते, जवळजवळ सर्वच प्रारूपांच्या उकलीमध्ये उतार किंवा चढाव प्रवणता (ग्रेडिएंट डिसेंट) या तंत्राचा वापर केला जातो. गंमत म्हणजे. उतार किंवा चढाव प्रवणता ही अकरावी किंवा बारावीत शिकलेल्या डेरिव्हेटीव्ह या संकल्पनेवर आधारित आहे. आपल्याला माध्यमिक शाळेत किंवा कनिष्ठ महाविद्यालयामध्ये शिकलेल्या गणिताचे उपयोग सहसा सांगितले जात नाहीत आणि त्यामुळे आपण ते निव्वळ परीक्षेपुरते वापरून विसरून जातो. आजची संकल्पना वाचल्यावर तुमच्या लक्षात येईन की, शाळकरी आणि कनिष्ठ महाविद्यालयीन वयात शिकलेल्या गणितीय संकल्पना किती उपयुक्त असतात.
देशभरातील इतर बातम्या वाचण्यासाठी येथे क्लिक करा
सकाळ+ चे सदस्य व्हा
ब्रेक घ्या, डोकं चालवा, कोडे सोडवा!
शॉपिंगसाठी 'सकाळ प्राईम डील्स'च्या भन्नाट ऑफर्स पाहण्यासाठी क्लिक करा.
Read latest Marathi news, Watch Live Streaming on Esakal and Maharashtra News. Breaking news from India, Pune, Mumbai. Get the Politics, Entertainment, Sports, Lifestyle, Jobs, and Education updates, मराठी ताज्या बातम्या, मराठी ब्रेकिंग न्यूज, मराठी ताज्या घडामोडी. And Live taja batmya on Esakal Mobile App. Download the Esakal Marathi news Channel app for Android and IOS.